large

Review Article

A New Approach to Listing Combinatorial Algorithm of Cnr

Nguyen Dinh Lau*

Department of Information Technology, University of Education and Science, University of Da Nang, Da Nang, Vietnam

Address for correspondence: Nguyen Dinh Lau, Department of Information Technology, University of Education and Science, University of Da Nang, Da Nang, Vietnam. E-mail: ndlau@ued.udn.vn
Submitted: 28-04-2021, Accepted: 07-05-2021, Published: 30-06-2021

ABSTRACT

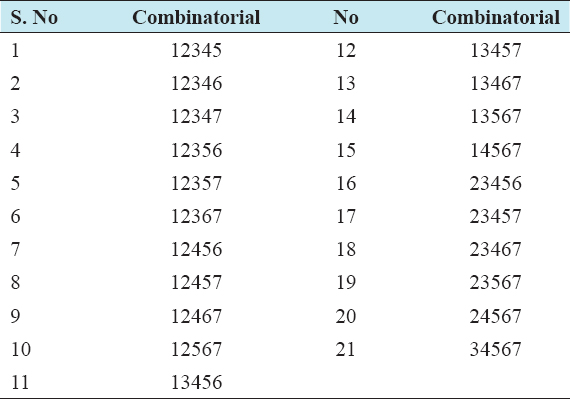
This paper aims at constructing listing combinatorial Algorithms of Cnr. Cnr is replaced by Cnr. This is the most common and appealing problem in discrete maths. The Cnr listing combinatorial problem is solved by exploiting many different techniques: Using generation and backtracking. The most possible complexity is O(r.Cnr). In this new approach, an attempt was made to find the subset of k elements in the set of m elements. The main content in the paper is based on the generation combinatorial algorithm of a smaller set. This will reduce the computation time as compared to the initial set n and r.

Keywords: Listing, Combinatorial, Generation, Algorithms, Subsets

INTRODUCTION

Listing combinatorial problems are common problems in discrete maths and have been applied to solve real problems such as: Queens, course breakdown, and others. However, when the input data are huge, the complexity is extremely large. For example: With input n = 20, r = 5, the complexity of set Cnr is 15504. It is, therefore, essential to propose algorithms with a new approach to improve the complexity.

The author has conducted in-depth studies in combinatorial algorithms and had many articles related to this field published widely nationally and internationally. Permutation and parallelization are discussed in the work named the problem of permutation and parallelization,[1] improved computing performance for listing combinatorial algorithms using multi-processing message passing interface (MPI) and Thread library[2] was also presented and published.

In the world, combinatorial algorithms have attracted attention of numerous researchers. The authors in Stojmenovic,[3] Akl et al.,[4] Akl and Stojmenovic,[5] Chen and Chern,[6] Djokic et al.,[7] Elhage and Stojmenovic,[8] Elhage and Stojmenovic,[9] discussed and proposed parallel listing combinatorial algorithms that specifically develop a parallel listing combinatorial algorithm of set Cnr.

This paper is underpinned by generation algorithm to build new listing combinatorial algorithms by dividing a set into different subsets to find the combinatorial sequence.

It is hoped that this article has made some new contributions to listing combinatorial Algorithms by constructing new listing combinatorial algorithm; giving correct proof; demonstrating complexity; and giving illustrative and comprehensive examples.

LISTING COMBINATORIAL ALGORITHMS OF (CNR)

Ideas

Suppose we consider the set r with n elements (1,2,…, n). Because the combinatorial is a set of elements without order, it is represented in a list, i.e, (s1, s2,…, sr) for s1 <s2 <… <sr. Thus, in dictionary order, the first combinatorial is (1, 2,…, r) and the last combinatorial is (n−r+1, n−r+2,…, n).

For example: Consider the set r = 5, n = 7 [1,2,3,4,5,6,7]. The first combinatorial is [1,2,3,4,5]. The next combinatorials are [1,2,3,4,6] and [1,2,3,4,7], [1,2,3,5,6], [1,2,3,5,7] and others. The final combinatorial is [3,4,5,6,7]. It is crucial to find the next combinatorial of [1,3,4,6,7]. It can be seen that there is no combinatorial with the first three elements 1,3,4 bigger than [1,3,4,6,7]. Thus, the next combinatorial must have the first three elements 1, 3, 5 and we have the next five element combinatorial [1,3,5,6,7].

How to Find the Next Combinatorial

Let α = {s1, s2,…, sr}, we find the next combinatorial β = {t1, t2., tr}.

First of all, it can be observed that the ith element in the combinatorial cannot exceed n−r+i because n−r+i is considered the maximum value of the ith element. We find m = max {i | si < n− r+i} Then we have

ti = si for i = 1, 2., m−1

tm= sm + 1

tm+i = sm + i + 1 for i =1, 2., r−m

Algorithm

  • Input: r, n

  • Output: a list of combinatorial of Crn with increasing order.

    Steps:

    Generation (int n, int r)

    • {

    • While (s[1]! = n-r+1)

    • {

    • printcombinatorial(r)

    • cout<<endl;

    • int m=0;

    • for (int i=r; i>=1; i--)

    • if(s[i]<n-r+i)

    • {

    • m=i;

    • break

    • }

    • s[m]=s[m]+ 1

    • for (int i=m+1; i<=r; i++)

    • s[i]=s[i-1] +1;

    • }//while

There is Cnrth loop of while (line 2), and there is rth loop of for (line 7). Thus, we have complexity O(r. Cnr).[10]

A NEW APPROACH TO CONSTRUCT LISTING COMBINATORIAL ALGORITHM OF CNR

New Ideas

It can be seen that the bigger the complexity O(r. Cnr) of the listing combinatorial algorithm of Cnr with gets, the more the n elements increase. Therefore, the author suggests constructing new listing combinatorial algorithm by finding every single subset. For each subset, Ai contains fixed first elements of combinatorial while unfixed last elements of combinatorial are in Ri⊂Xi (Ri as set listing combinatorial Cmk), where m = |Xi|, m <n and k <r. The Ai and Xi are defined in the following section.

New Approach

Hence, n = 7, r = 5 then Cnr = 21.

It is time to divide and allocate elements of combinatorial for Ai and Xi [Table 1].

Table 1: Listing combinatorial of C75

thumblarge

Analysis 1

  • Let X1 = {3,4,5,6,7}. Let A1 with 2 first elements {1,2}∪ R1 (R1⊂X1, card (R1) =3). R1 as set listing combinatorial Cmk (m = 5, k = 3), Cmk=C53=10 with 10 combinatorial as in Table 2

  • Let X2 = {4,5,6,7}. Let A2 with 2 first elements {1,3}∪R2 (R2⊂X2, card (R2) =3). R2 as set listing combinatorial Cmk (m = 4, k = 3), Cmk=C43=4 with 4 combinatorial as in Table 2

  • Let X3 = {5,6,7}. Let A3 with 2 first elements {1,4}∪R3 (R3⊂X3, card (R3) =3). R3 as set listing combinatorial Cmk (m = 3, k = 3), Cmk=C33=1 with 1 combinatorial as in Table 2

  • Let X4 = {4,5,6,7}. Let A4 with 2 first elements {2,3}∪R4 (R4 ⊂4, card (R4) =3). R4 as set listing combinatorial Cmk (m = 4, k = 3), Cmk=C43=4 with 4 combinatorial as in Table

  • Let X5 = {5,6,7}. Let A5 with 2 first elements {2,4}∪R5 (R5⊂X5, card (R5) =3). R5 as set listing combinatorial Cmk (m ⊂ 3, k = 3), Cmk=C33=1 with 1 combinatorial as in Table 2

  • Let X6 = {5,6,7}. Let A6 with 2 first elements {3,4}∪R6 (R6⊂X6, card (R6) =3). R6 as set listing combinatorial Cmk (m = 3, k = 3), Cmk=C33=1 with 1 combinatorial as in Table 2.

Table 2: Listing combinatorial of C75 equa to Ai∪Ri

thumblarge

Analysis 2

Subset Ai (i=1, 2,…, 6) B= {1,2,3,4}. |Ai|=2

Analysis 3

Subset general A can be identified as follows:

Let n, r. Ai (i=1,2,3,…,C(n-r+int(r/2),int(r/2))) ⊂ B={1,2,…,n-r+int(r/2). With |Ai|=int(r/2), |B|=n-r+int(r/2).

Analysis 4

Suppose that Ai[int(r/2)] is the value of the last element of Ai. When n=7 and r = 5, we have:

A1[int(r/2)] = A1 [2] = 2

A2[int(r/2)] = A2[2] = 3

A3[int(r/2)] = A3[2] = 4

A4[int(r/2)] = A4[2] = 3

A5[int(r/2)] = A5[2] = 4

A6[int(r/2)] = A6[2] = 4

Analysis 5

Xi can be identified from Ai as follows:

Xi={Ai[int(r/2)] + 1, Ai[int(r/2)] + 2,…, n}

Theorem 1

|α| =|Ai∪Ri|=r, with |Ri|= r-int(r/2), Ri ⊂Xi

Proof

The number of elements of combinatorial of Cnr is r, because |Ai| = int(r/2) and |Xi| = r-int(r/2) then the total number of combinatorial = int(r/2)+r-int(r/2)=r.

Analysis 6

The example shows that the number of combinatorial is the times to get three elements in Xi (I = 1, 2,…, 6). It means that the number of combinatorial = 6

C53+C43+C33

+C43+C33

+C33

=10+4+1+4+1+1=21=C75.

In general, we have the number of combinatorial as follows:

[C(n-int(r/2),r-int(r/2))+ 2.C(n-int(r/2)-1,r-int(r/2))+

3.C(n-int(r/2)-2),r-int(r/2))+…+ r-int(r/2)C(n-int(r/2)-n+r),r-int(r/2))]+

[C(n-int(r/2)-1,r-int(r/2))+2C(n-int(r/2)-2),r-int(r/2))+…+r-int(r/2)C(n-int(r/2-n+r),r-int(r/2))] +…+ [C(n-int(r/2)-n+r),r-int(r/2))]

Similarly, the number of new Approach listing combinatorial equa to Cnr.

Hence, there are two main steps to construct new listing combinatorial algorithm:

  • Initialize subset Ai. |Ai| =int(r/2), Ai⊂B = {1, 2,…, n-r+int(r/2), |B|=n-r+int(r/2).i=1, 2, 3,…, C(n-r+int(r/2), int(r/2))

  • For Ai: Print Ai∪Ri with |Ri|= r-int(r/2), Ri ⊂Xi.

Constructing New Listing Combinatorial Algorithm

Input: n, r

Output: Print all listing combinatorial of Cnr

  • Let Ai listing combinatorial C(n-r+int(r/2), int(r/2))

  • For Ai (i=1,2,3,…, C(n-r+int(r/2), int(r/2)). Initialize Xi={Ai[int(r/2)] + 1, Ai[int(r/2)] +2,…, n}

  • For Ai (i=1,2,3,…, C(n-r+int(r/2), int(r/2)).Print all listing combinatorial Ai∪Ri with |Ri|= r-int(r/2), Ri ⊂Xi.

Theorem 2

Max(|Xi|) =|X1|

Proof

As defined above A1 = {1, 2,…, int(r/2) hence A1[int(r/2)] = int(r/2) is the minimum. We have min(A1[int(r/2)], A2[int(r/2)],…, AC(n-r+int(r/2),int(r/2) [int(r/2)])= A1[int(r/2)]. Since A1[int(r/2)], A2[int(r/2)],…, AC(n-r+int(r/2),int(r/2) [int(r/2)] are the last elements of Ai (i=1,2,3,…, C(n-r+int(r/2), int(r/2)), then A1[int(r/2)] is the minimum. It can be deduced that |X1| is the maximum and Max(|Xi|) =|X1|.

Theorem 3: The complexity

Max{O(int(r/2).C(n-r+int(r/2),int(r/2))),O(r- int(r/2).C(n- int(r/2), r-int(r/2)))}

Proof

Initialize Ai including combinatorial C(n-r+int(r/2), int(r/2)) then the complexity is O(int(r/2).C(n-r+int(r/2), int(r/2)))

According to theorem 2, Max(|Xi|) =|X1| hence the combinatorial r-int(r/2) from X1 is the maximum. We also have X1= {A1[int(r/2)]+1, A1[int(r/2)]+2,…,n}={int(r/2)+1, int(r/2)+2,…,n} then the number of elements of X1 is |X1|=n- (int(r/2)+1)+1=n- int(r/2). It can be deduced that the complexity to identify combinatorial r-int(r/2) from X1 is O(r-int(r/2).C(n- int(r/2), r-int(r/2))).

Finally we have the complexity Max{O(int(r/2).C(n-r+int(r/2),int(r/2))),O(r-int(r/2).C(n- int(r/2), r-int(r/2)))}.

Analysis 7

The complexity of the combinatorial algorithm is O(r.Cnr).

According to theorem 3, the complexity of the new listing combinatorial algorithm is: Max{O(int(r/2).C(n-r+int(r/2),int(r/2))),O(r- int(r/2).C(n- int(r/2), r-int(r/2)))}.

Case 1: If O(int(r/2).C(n-r+int(r/2),int(r/2)))>O(r- int(r/2).C(n- int(r/2), r-int(r/2)))

Then the complexity of the new listing combinatorial algorithm is:

O(int(r/2).C(n-r+int(r/2), int(r/2)))

The complexity ≤ O(r.C(n, r)), it can be seen that

O(int(r/2).C(n-r+int(r/2), int(r/2))) < O(r.C(n, r))

Case 2: If O(int(r/2).C(n-r+int(r/2),int(r/2)))<O(r-int(r/2).C(n- int(r/2), r-int(r/2)))

Then the complexity of the new listing combinatorial algorithm is:

O(r- int(r/2).C (n- int(r/2), r-int(r/2)))

The complexity -iO(r.C(n, r)), it can be seen that

O(r- int(r/2).C (n- int(r/2), r-int(r/2)))

< O(r.C (n,r))

Thus, in both cases, the complexity of the new listing combinatorial algorithm is smaller than the complexity of the previous combinatorial algorithm.

CONCLUSION

In this paper, the author has built a new listing combinatorial algorithm of Cnr within a new approach. In particular, the author also analyzed the algorithm logically and also proved 3 theorems related to the new algorithm.

Last but not least, the paper proves that the complexity of the new listing combinatorial algorithm is smaller than that of existing combinatorial algorithm.

The further development of this study involves building parallel algorithms on the environment MPI, Cuda, Map/Reduce then, analyzing and comparing the complexity on different processors and on different input data sets to further reduce the complexity and constructing other combinatorial enumeration algorithms to reduce computation time for permutation, combinatorial, and binary sequence algorithms in discrete maths.

REFERENCES

1.  Lau ND. Parallel Algorithm List Permutations, Quy Nhon, Binh Dinh, Vietnam;2017. p. 348-53.

2.  Lau ND. Improved computing performance for listing combinatorial algorithms using multi-processing MPI and thread library. Int J Comput Sci Inf Technol 2018;10:16.

3.  Stojmenovic I. Listing combinatorial objects in parallel. Int J Parallel Emergent Distrib Syst 2006;21:127-46.

4.  Akl SG, Gries D, Stojmenovic I. An optimal parallel algorithm for generating combinations. Inf Proc Lett 1989;33:135-9.

5.  Akl SG, Stojmenovic I. Parallel algorithms for generating integer partitions and compositions. J Comb Math Comb Comput 1983;13:107-20.

6.  Chen GH, Chern MS. Parallel generation of permutations and combinations. BIT Numer Math 1986;26:277-83.

7.  Djokic B, Miyakawa M, Sekiguchi S, Semba I, Stojmenovic I. Parallel algorithms for generating subsets and set partitions. In:Asano T, Ibaraki T, Imai H, Nishizeki T, editors. Vol. 450. Proceedings of SIGAL International Symposium on Algorithms. Tokyo, Japan:Lecture Notes in Computer Science;1990. p. 76-85.

8.  Elhage H, Stojmenovic I. Systolic generation of combinations from arbitrary elements. Parallel Proc Lett 1992;2:241-8.

9.  Kapralski A. New methods for the generation of permutations, combinations, and other combinatorial objects in parallel. J Parallel Distrib Comput 1993;17:315-26.

10.  Torres M, Barrera J. A parallel algorithm for finding small sets of genes that are enough to distinguish two biological states. Genet Mol Biol 2004;27:686-90.