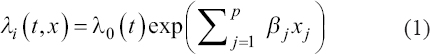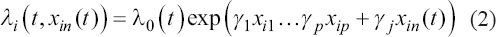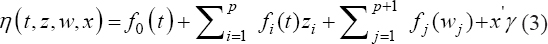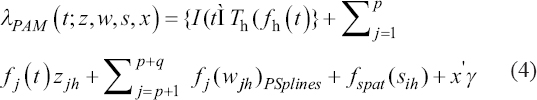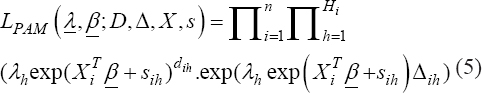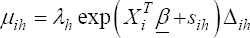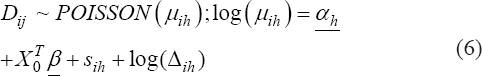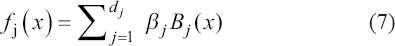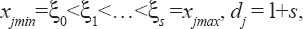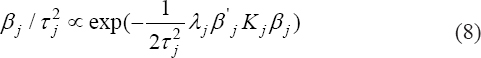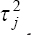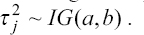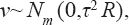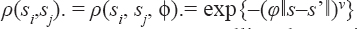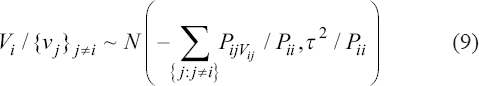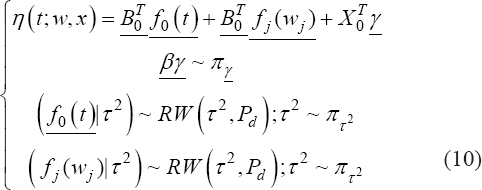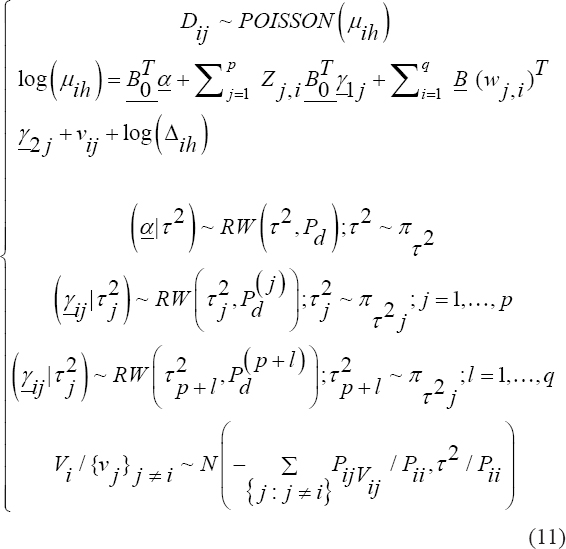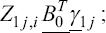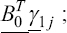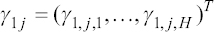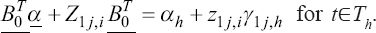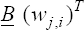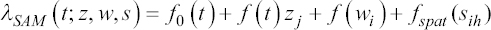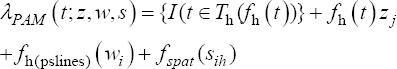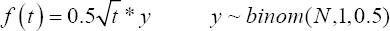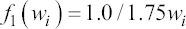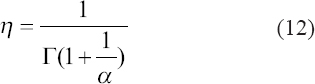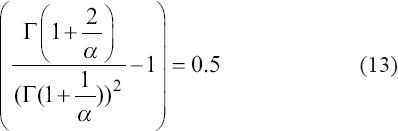A piece-wise additive model of survival data with non-linear rut
Omaku Peter Enesi1*, B. A. Oyejola2
1Department of Mathematics and Statistics, Federal Polytechnic, Nasarawa, Nigeria, 2Department of Statistics, University of Ilorin, Ilorin, Nigeria
ABSTRACT
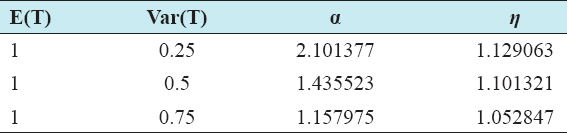
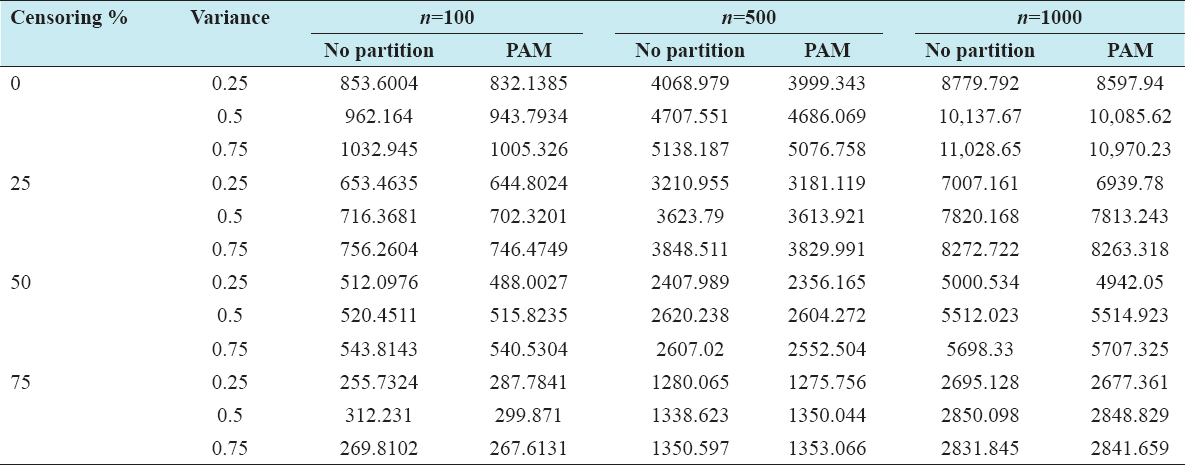
A critical step when developing multivariate risk prediction models is to decide which are the predictors that should be included and which ones could be neglected to get an accurate but interpretable model. The general additive models (GAMs) have come as quite an attractive procedure to handle covariate complexities in their various functional forms which is unlikely with the Cox model. In this study, a modification of piece-wise additive hazard model is proposed. Three levels of variance of Weibull distribution were assumed for baseline hazards in generating the data. The sensitivity of the baselines was accessed under four censoring percentages (0%, 25%, 50%, and 75%) and three sample sizes (n=100, 500, and 1000), for when models were single additive model (SAM) and when partitioned – piece wise additive model (PAM). A piece-wise Bayesian hazard model with structured additive predictors in which time-varying covariate and the functional form of continuous covariates were incorporated in a non-proportional hazards framework was developed. Hazard function was modeled through additive predictors that are capable of incorporating complex situations in a more flexible framework. Analysis was done utilizing MCMC simulation technique. Results revealed that the PAMs in most situations outperformed the SAMs with smaller DIC values and larger predictive powers with the log pseudo-marginal likelihood criterion.
Keywords: Continuous covariate functions, generalized additive model, penalty splines, piece-wise additive model, proportional hazard, single additive model, time-varying covariates