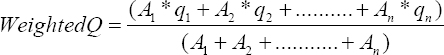Geospatial technique for runoff estimation based on soil conservation service curve number method in upper Cauvery Karnataka
Mohammed Badiuddin Parvez*, Amritha Thankachan, K. Chalapathi, M. Inayathulla, E. Chithaiah,
Department of Civil Engineering, University Visvesvaraya College of Engineering, Bengaluru University, Bengaluru, Karnataka, IndiaABSTRACT
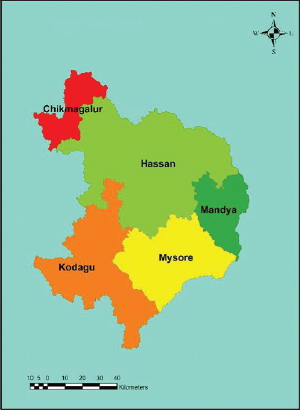
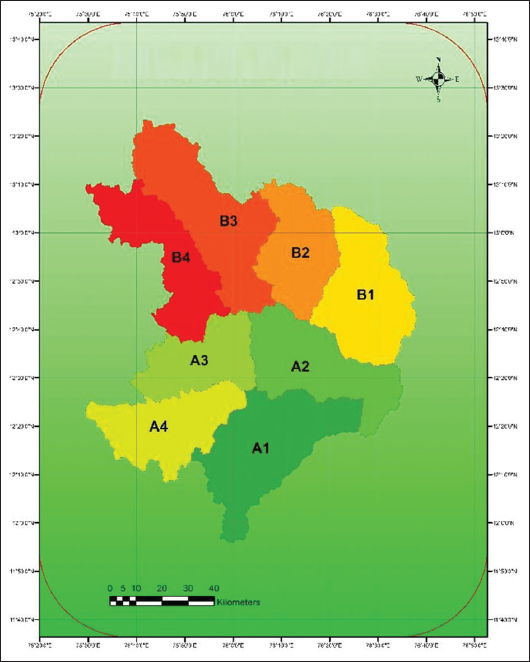
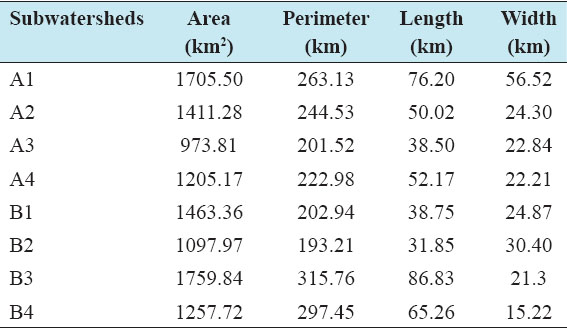
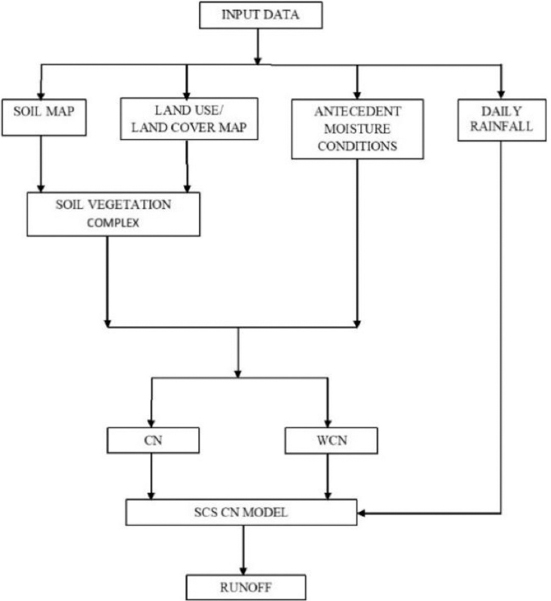
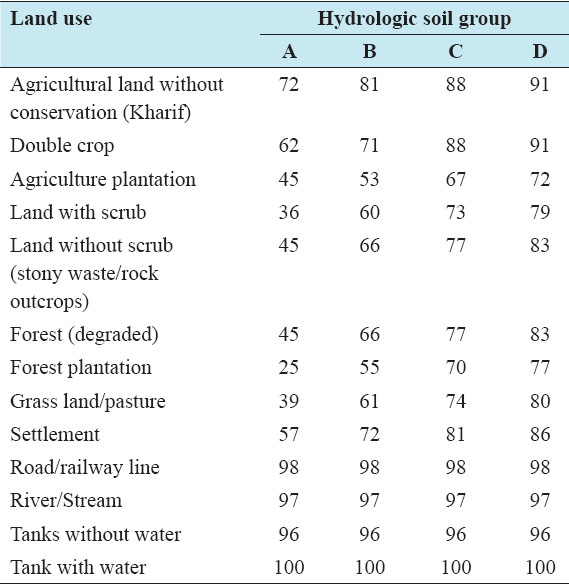
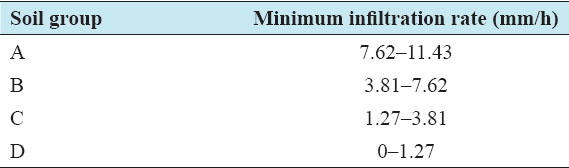
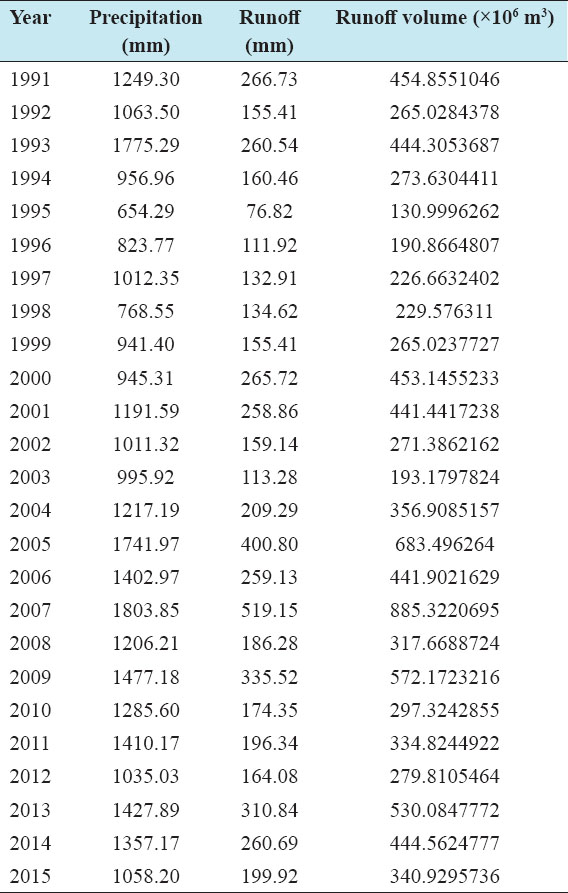
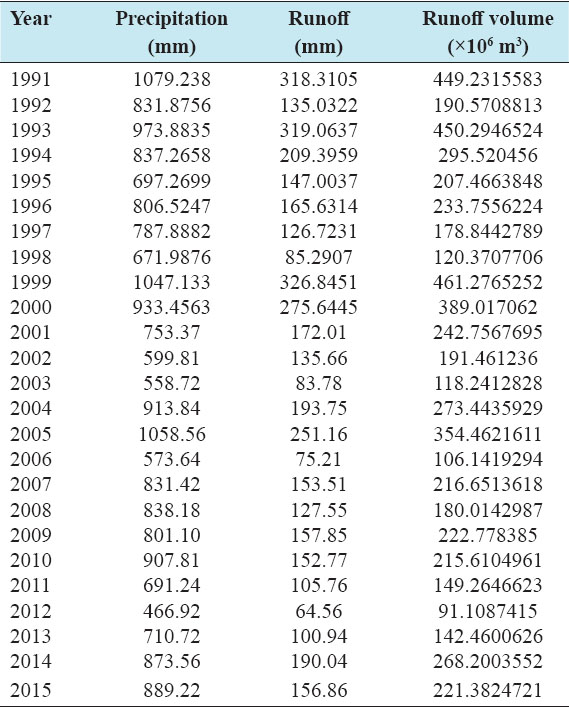
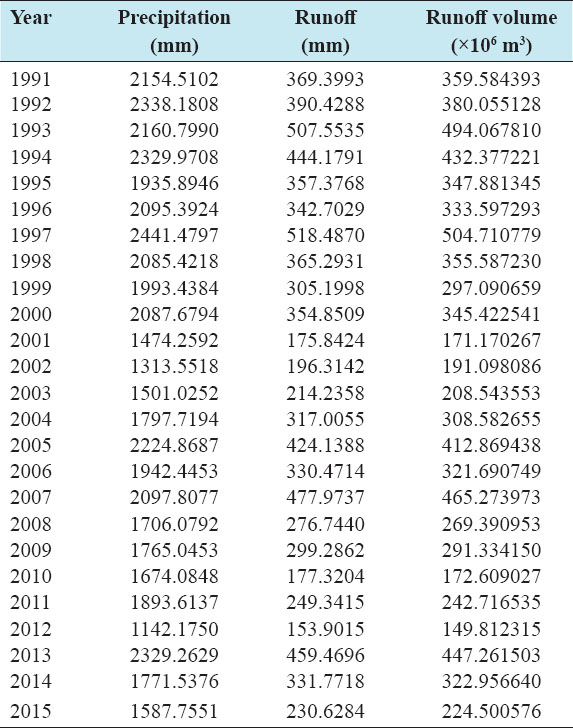
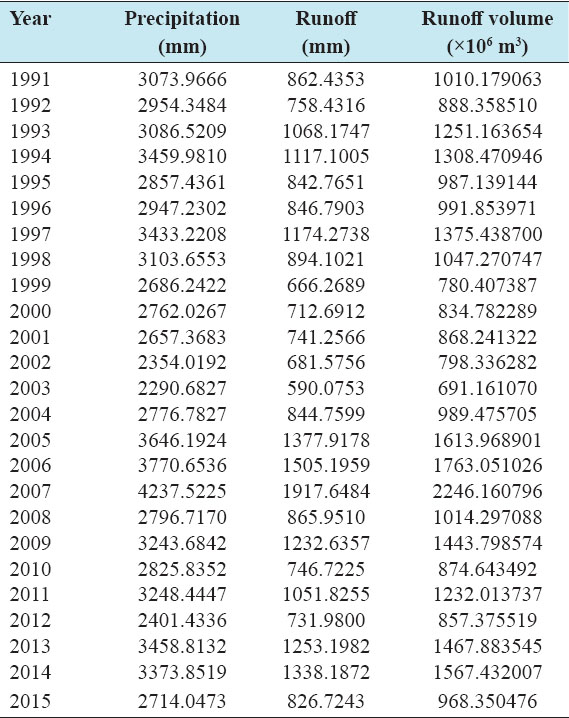
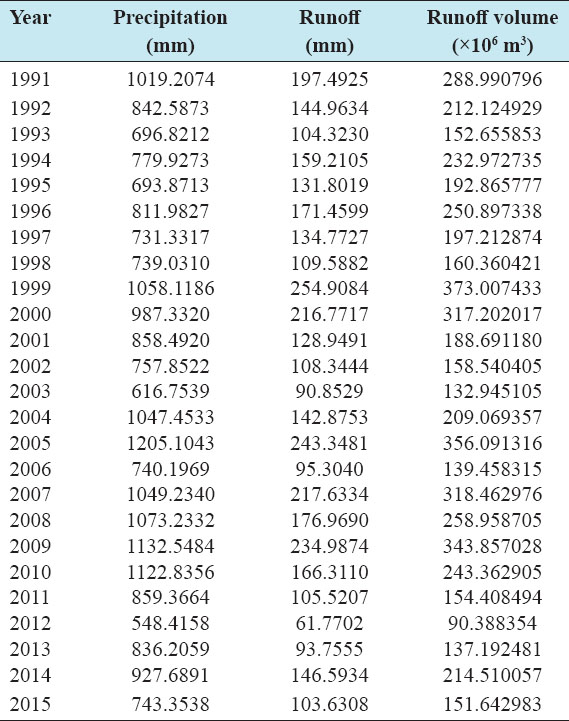
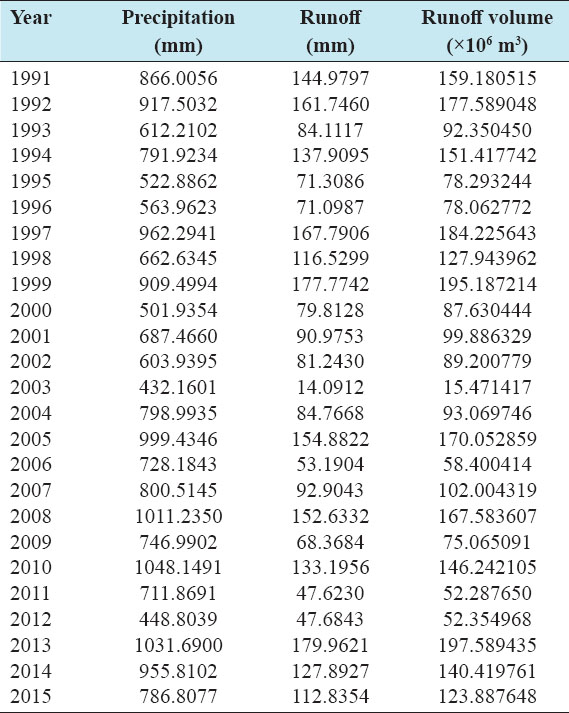
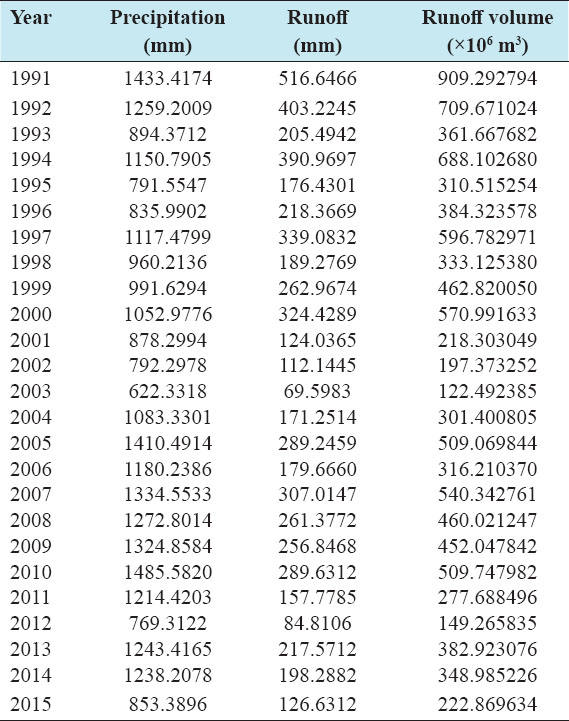
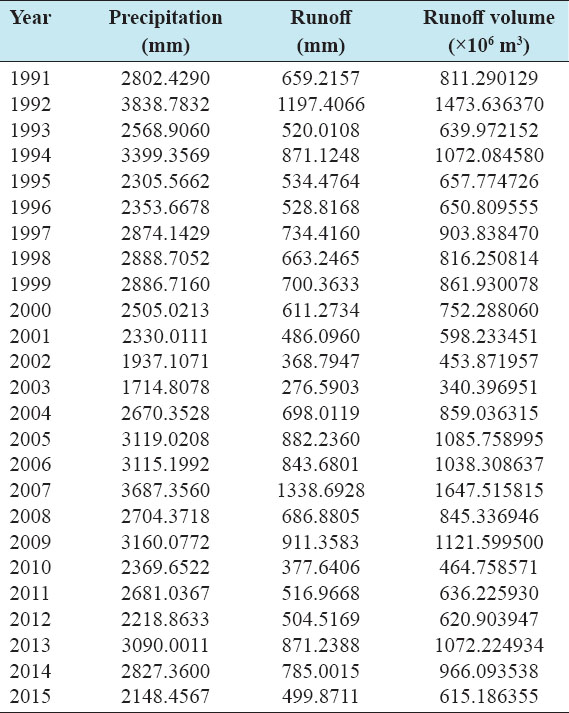
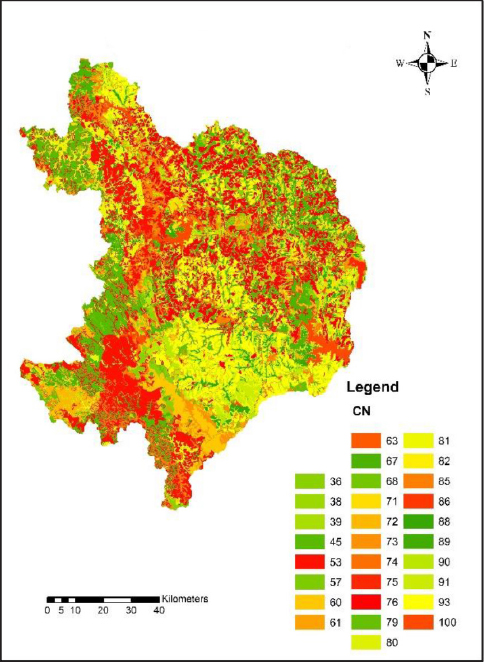
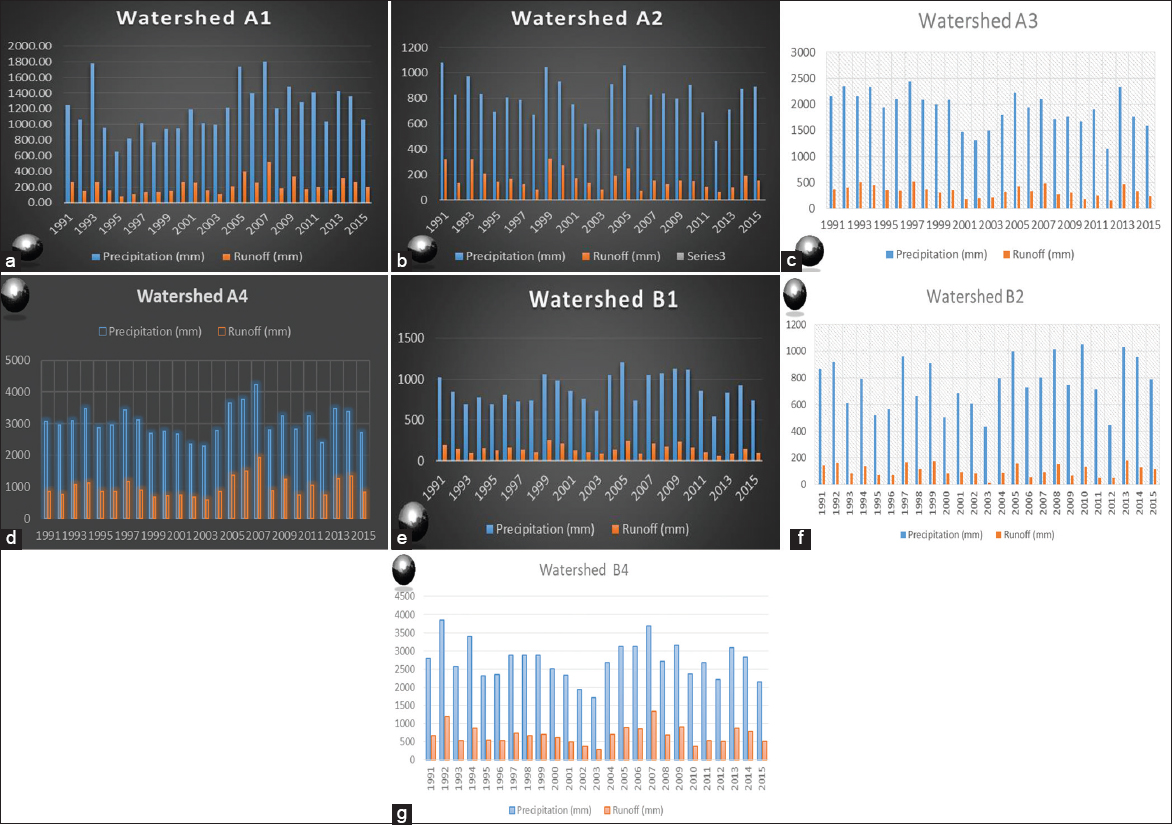
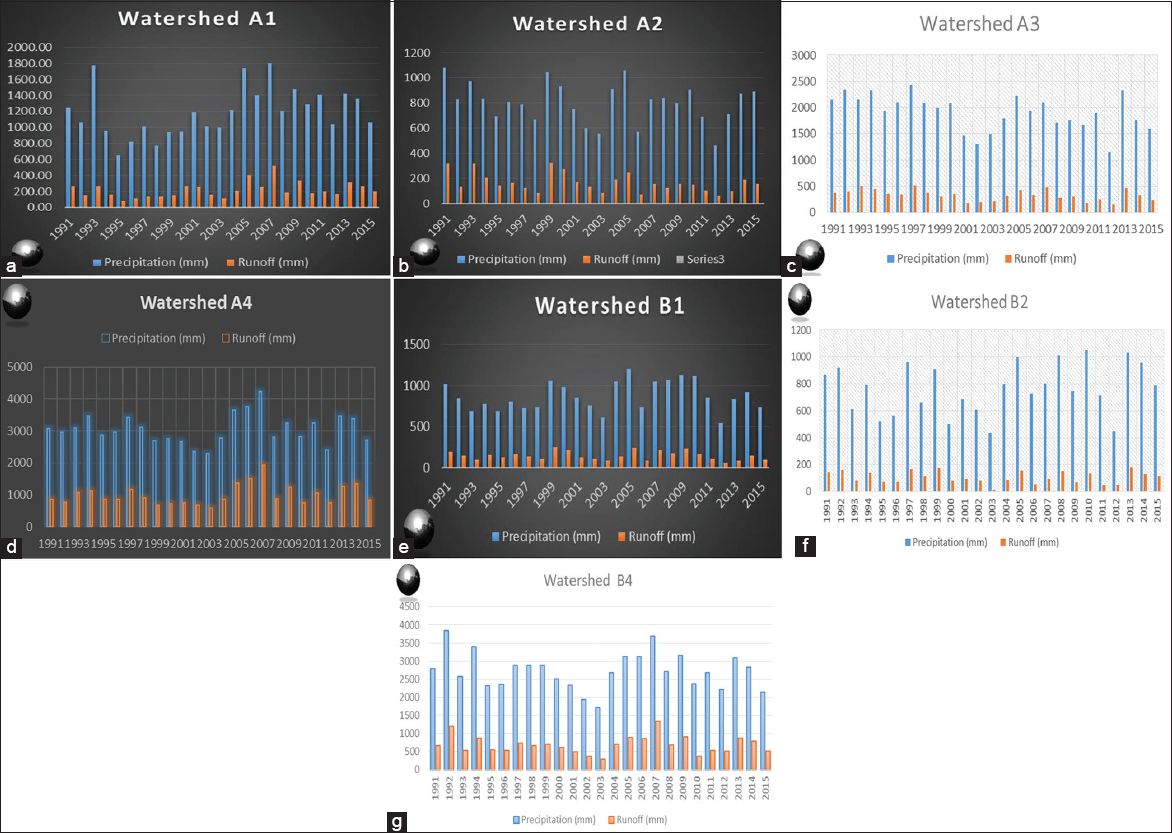
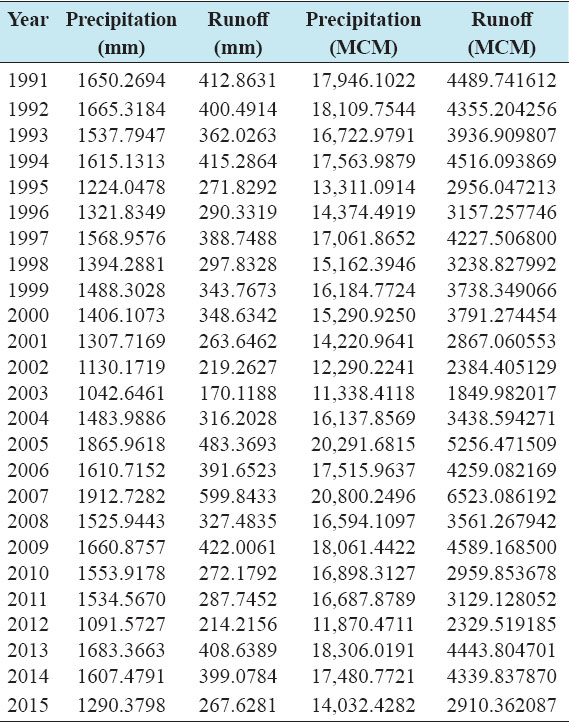
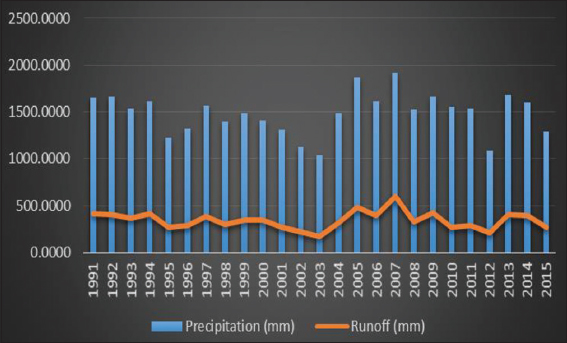
Accurate estimation of runoff and sediment yield amount is not only an important task in physiographic but also important for proper watershed management. Watershed is an ideal unit for planning and management of land and water resources. Direct runoff in a catchment depends on soil type, land cover, and rainfall. Of the many methods available for estimating runoff from rainfall, the curve number (CN) method (soil conservation service CN [SCS-CN]) is the most popular. The CN depends on soil and land use characteristics. This study was conducted in the upper Cauvery Karnataka using remote sensing and geographic information system (GIS). SCS-CN method has been used for surface runoff estimation for eight watersheds of upper Cauvery. The soil map and land use were created in the GIS environment because the CN method is used here as a distributed model. The major advantage of employing GIS in rainfall-runoff modeling is that more accurate sizing and catchment characterization can be achieved. Furthermore, the analysis can be performed much faster, especially when there is a complex mix of land use classes and different soil types. The results showed that the surface runoff ranged from 170.12 to 599.84 mm in the study area when rainfall rates were received from 1042.65 to 1912 mm. To find the relationship between rainfall and runoff rates, the straight-line equation was used. That was found that there was a strong correlation between runoff and precipitation rates. The value correlation coefficient between them was 86%. The average depth of runoff is more in watershed A4, the average runoff coefficient is less in watershed B2, and the correlation coefficient is high in A4 to a value of almost 89.5%.
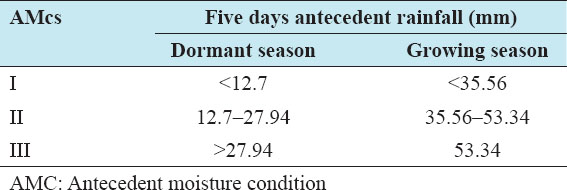
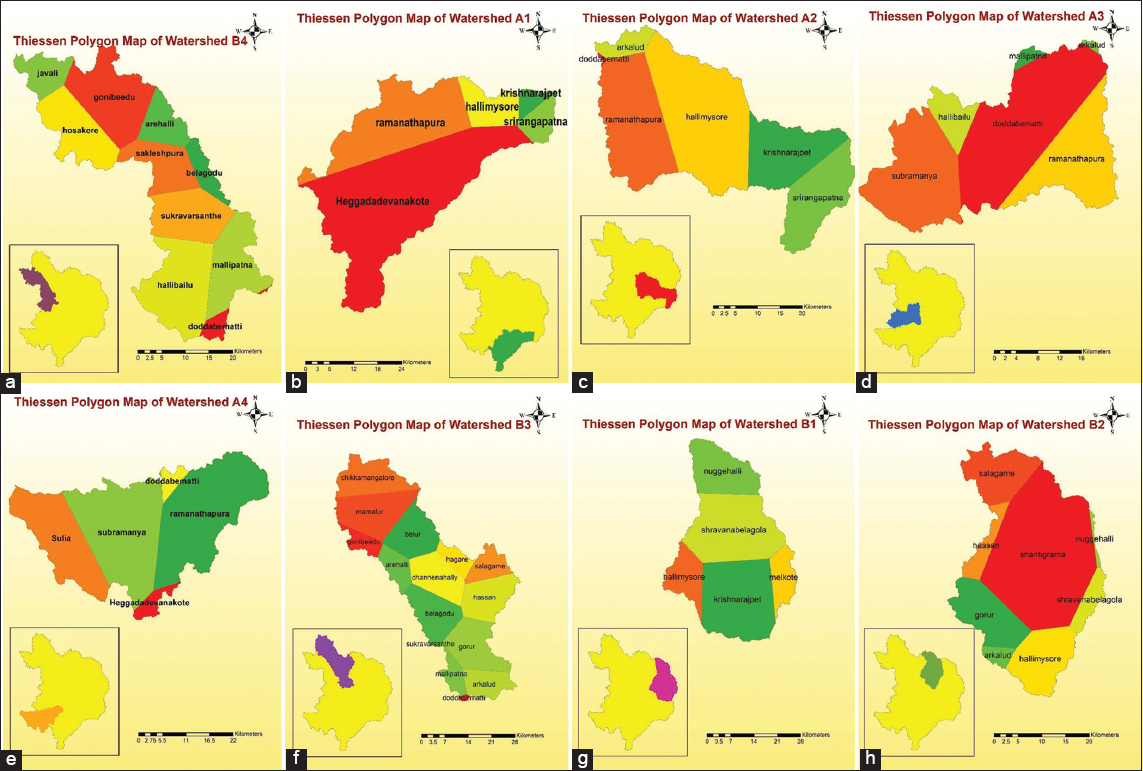
Keywords: Antecedent moisture condition, curve number, infiltration, rainfall, runoff, Thiessen polygon